Production Economic Principles

In the book Finance and the Farmers (Van Zyl, J(et al) of Standard Bank, planning is defined as “ the managerial task that involves purposeful deliberation on the future objectives of a business or a section thereof, the means and activities involved, the problems that may be experienced and the formulation of the most suitable plan of action for the attainment of these goals”

Production planning primarily involves making choices and decisions - that means - selecting the most profitable and sustainable alternative for your production enterprise from other passable alternatives. There are many risks and uncertainties associated with farming. Detailed planning is therefore absolutely necessary. There are, as mentioned earlier, many factors that influence the production process and to assist the farmer or manager to make the correct decisions, production economics must be used and understood to assist with decision making.

Production economic principles comprise a set of norms or rules that will ensure that choices or decisions will lead to maximum profit. The rules are applied in the following order or steps:

• Obtain and collect physical and biological data and process it into useful information
• Collect price data for the commodities produced and process it in useful data
• Apply the relevant economic rules regarding decision making to achieve maximum profit

Marginality

Marginality is a very important concept in production economics. It explains how changes will affect a farming business - how changes in one factor will affect the profit or the economic situation as a whole - or how will the applications of additional fertiliser affect the crop results?

Marginality refers to an alteration of one factor (increase or decrease) in a process as the cause of the change of another factor - what will the additional income be? Marginal changes are calculated by determining the difference between the original value and the new value which resulted from the change in the controlling factor. The change in the input is indicated with Δ (the Greek letter delta)

E.g., changes in wheat production = Δ wheat production and Δ fertiliser

The second important concept in production economics is the production faction. The production function indicates the relationship between different quantities or amounts of specific output and a specific input, while all the other outputs stay the same or constant. This production function can be presented as a table, a graph or a mathematical equation.

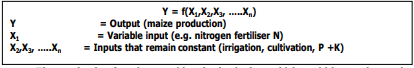
The production function provides the basic data which could be used to make deductions from production.

The Total Production (TP) and the input level are required to determine the production. It can also be used to calculate the average production and the marginal production.

Average production is the total production divided by the input level. It is the production per input unit. The Average production will increase and then decrease as more units of the input is required.

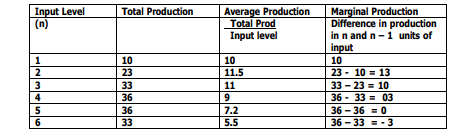
The marginal production (MP) is the difference between the total productions (23 – 33 = 13), divided by the difference in the input level (2-1=1)

If 20 kg of N is applied, the average production will be 11.5 kg while the marginal production will increase to 13 kg. For every kg of N fertiliser added, the yield will increase with 13 kg up to 30 kg of N where the yield will only increase by 10 kg per kg N applied This can be illustrated in a graph.

Graph 1: Typical production function in Agriculture

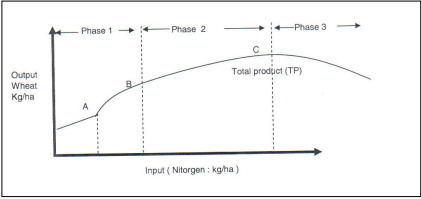
Production in the first phase indicates that the average production (AP) constantly increases. The marginal production (MP) is higher than the average.

Production: Maximisation of profit occurs constantly by adding additional units of fertilizer.

Graph 2: Marginal production and average Production

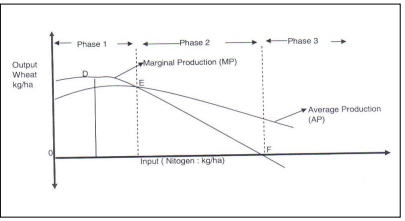
In the second phase, the total production rate still increases, although in a decreasing way until it reaches point C where the increasing rate equals zero. The average production (AP) curve decreases throughout, as does the Marginal production (Mp) curve. The MP lies below the AP curve and MP = 0 at the point.

Point F correlates with point C on graph 1.

In the third phase, the total production starts to decline which means the MP curve is negative from point F onwards.

Diminishing Marginal Returns

The law of diminishing returns states that, as additional units of a variable input are applied in combination with one or more fixed input(s), the marginal returns will eventually start to decrease.

For further evaluation of the production function the:

Input/output ration: - how much input or how much production is necessary to determine the most profitable input or production level.

Profit involves money – thus, to maximise profits, income and costs must be considered. The price of inputs and output (product) must be known. The golden rule for decision making is: The optimum input application level or the optimum production level is the level at which the maximum profit is achieved. For maximum profit, the marginal income (MI) should be equal to the marginal cost (MC).

Input/input ratios: - how to produce. The question to be asked is “Will another input combination produce the same result at a lower cost?” Will it be possible to substitute one input with another? Four rates of substitution are possible:

• A fixed rate of substitution uses inputs in the production process according to a fixed ratio and no other substitution takes place - e.g., the seed is treated with a specific fungicide or pesticide and non-other.
• A constant rate of substitution is where one input X1 can always be substituted in the same ratio with other inputs X2 in order to generate the same production - e.g., replacement of fertiliser with compost or manure at a constant rate of 5 parts manure to1part fertiliser
• An increasing rate of substitution is where the quantity of input X1 increases, fewer and fewer units of X2 must be used to replace one unit of input X1. E.g., LAN fertiliser is needed for nitrogen, but urea can be used that is cheaper as long as it is done in the correct ration, as urea contains more N as LAN per unit.
• A decreasing rate of substitution: - as the quantity of X1 decreases, more and more units of X2 is required to replace one unit of input X1 - e.g., the use of grazing (X1 ) in comparison to a concentrate (X2) to produce milk - as the grazing decreases in nutritional value, the number of concentrates added to the cows’ diet must increase to maintain the same production level.

Output/ output ratios - what to produce? It is necessary to determine the physical relationship between products. The following output relations can occur:

Joint products - where the production of one product automatically generates the other e.g., wool and mutton

Supplementary products - are obtained where the change in the production of one product has no effect on the production of another product. e.g., beef cattle and goats

Complementary products - the increase in the production of one product also results in the increase of the production of the other e.g.

• (1) a combination of cattle and goats – goats prevent and control bush encroachment, thus making more grazing available to the cattle or
• (2) the crop rotation with leguminous plants will lead to higher production.

Antagonistic products - one product claims the 135, the input of another product with adverse effects - e.g., cattle and blue wildebeest cannot graze together as the wildebeest is the carrier of the disease bovine malignant catarrh (Snotsiekte) that is fatal to cattle.

Van Zyl J (et all) expresses the rule for decision making as Profit is maximised when two outputs or products are produced using a given number of limited inputs, where the physical rate of substitution of the two products is equal to the inverse price ratio of the products.