Properties of Geometric Shapes
Surface Area of Two-Dimensional Figures
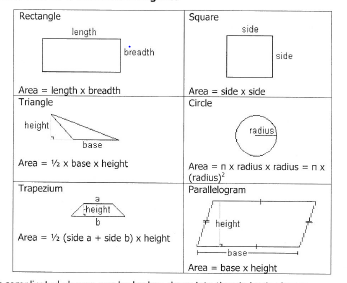
Most complicated shapes can be broken down into the six basic shapes shown above.
Calculate the surface area of the shape below.
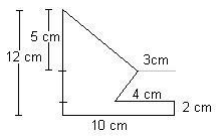
Step 1: Construct lines to divide the shape into any combination of the six basic shapes.
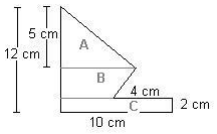
Step 2: Calculate the missing lengths
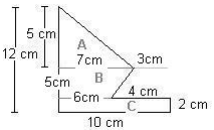
Step 3: Calculate the areas of shapes A, B and C
Area A (triangle) = ½ x base x height = ½ x 7cm x 5 cm = 32,5cm²
Area B (trapezium) = ½ (7cm + 6cm) x 5cm = ½ x 13cm x 5cm = 32,5cm²
Area C (rectangle) = length x breadth = 10cm x 2cm = 20cm² Step
Step 4: Add up Areas A, B and C to obtain total area
Total surface area = Area A + Area B + Area C
= 32,5cm² + 32,5cm² + 20cm²
= 85cm
Surface Area of 3-Dimensional Figures
To calculate the surface area of a three-dimensional figure, we need to break the shape up into known shapes by creating a net diagram. If you had to cut out the net and fold it, it would give you a 3-d shape.
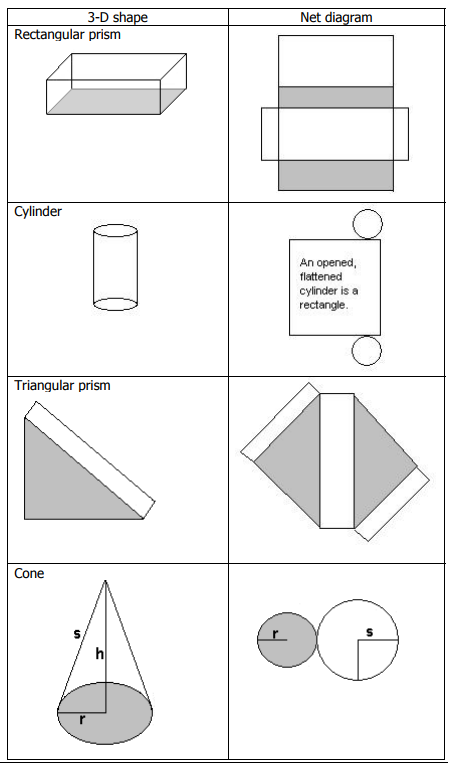
Calculate the surface area of the triangular prism below:
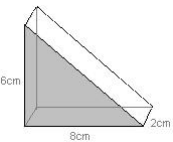
The length of the longest side of the triangle needs to be calculated by Pythagoras: Hypotenuse² = 6² + 8² = 36 + 64 = 100
Hypotenuse = 10cm
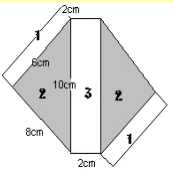
We prepare a net diagram:
Total surface area = 2 x area 1 + 2 x area 2 + area 3
= 2x2cm x 6cm + 2 x ½ x 8cm x 6cm + 2cm x 10cm
= 24cm² + 48cm² + 20cm² = 92cm
Volume of 3-Dimensional Figures
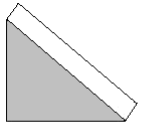
Many three-dimensional shapes are right prisms. If a right prism is cut into slices that run parallel to the base, then all the slices have the same cross section. A right prism can also be described as a three-dimensional shape in which the sides are at right angles to the base. All the sides must then have the same height. For example, the triangular prism is a right prism. The shaded area is the base, and the sides all form 900 with the base. The sides are all the same height.
 |
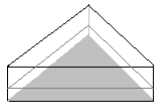 |
| The triangular prism is lying with its base pointing towards you. | The same prism is now lying on its base. The dark grey line indicates a slice that can be cut. The slice has the same shape as the base. The sides of the prism are all the same height. The sides are all perpendicular to the base. |
The rectangular prism, the cylinder, the triangular prism and a prism that has any other shape as its base are all right prisms. The cone and the sphere are NOT right prisms.
| 3-D shape | Volume |
|
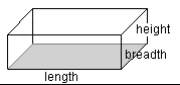
Rectangular prism
|
Volume = area of base x height = area of rectangle x height = length x breadth x height |
|
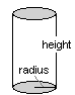
Cylinder
|
Volume = area of base x height = area of circle x height = π r² x height |
|
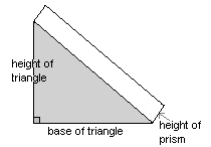
Triangular prism
|
Volume = area of base x height = Area of triangle x height of prism = ½ x base of triangle x height of triangle x height of prism |
|
Cone
|
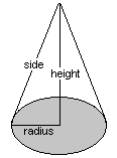
The volume of a cone is one third of the volume of a cylinder. Volume = (Area of Circle x height)/3 or = (π x r² x height)/3 |
|
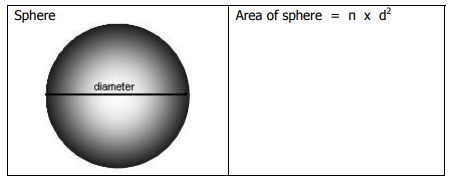
Sphere
|
Volume = π x (diameter)³ 6 |
Example:
A farmer needs to calculate the volume of a walk-through dip tank that he plans to build. The dimensions and shape are given in the drawing below.
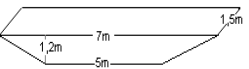
First, we need to identify the base of the prism. The base is a trapezium. Volume = area of base x height = area of trapezium x breadth of tank = ½ x (7m + 5m) x 1,2m x 1,5m = 10,8m
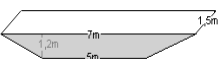
Example:
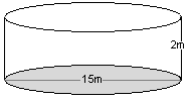
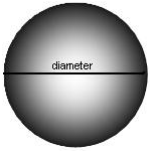
A farmer has a round water reservoir on his farm. He wants to work out how much water it holds. The reservoir has a diameter of 15m and is 2m deep.
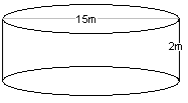
We need to identify the base. The base surface is either the top surface of the reservoir, or the bottom, i.e. it is a circle.
Now we need to calculate the radius.
The radius is half of the diameter, i.e. 7,5m
Volume = area of base x height
= area of circle x depth of tank
= π r² x depth of tank
= π x 7,5m x 7,5m x 2m
= 353,43m³