Calculating Heights and Distances
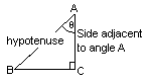
In the diagram below side c is called the hypotenuse. The hypotenuse is always the side opposite the 90° angle.
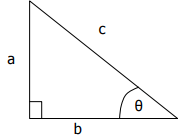
Pythagoras’ theorem states the following for a right-angled triangle: c2 = a2 + b2
In other words, Pythagoras’ theorem states: In a right-angled triangle the sum of the squares of the shorter two sides is equal to the square of the hypotenuse.
Example:
Calculate the size of the side marked x in each case.
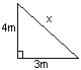 |
x2 = 42 + 32 = 16 + 9 = 25 x = 5m |
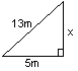 |
x2 + 52 = 132 x2 + 25 = 169 x2 = 169 – 25 = 144 x = 12m |
The sides of a right angles triangle can also be seen in relation to the other angles:
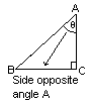
Side AC lies opposite angle B.
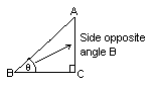
Side BC lies adjacent (next to) angle B
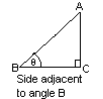
Notice that there are two sides adjacent to angle B: side AB and side BC. We do, however, already know that side AB is the hypotenuse. So only side BC is called “adjacent”.
Side AC lies adjacent to angle A.
Side BC lies opposite angle A.
Trigonometry laws are as follows:
|
sin θ = opposite/hypotenuse |
The trigonometric ratios must be learned. Learning tip: Remember this silly rhyme. The first letters of each word help you to remember. Some Old Hags Cackle And Haggle Till Old Age |
In triangle ABC, we can work out the three trig ratios.
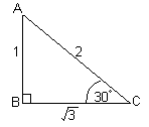
Sin 30° = o/h = ½ = 0,5
Cos 30°= a/h = √3/2 = 0,867
Tan 30°= o/h = 1/3 = 0,33
Now use a scientific calculator and work out sin 30°. You get 0,5.
(key sequence on a calculator: sin 30 =)
Work out cos 30°and you get 0,867
Work out tan 30°and you get 0,33.
These trigonometric ratios can be used to work outsides and angles of right-angled triangles.
Example:
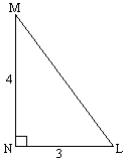 |
Work out all the missing sides and angles in the triangle MNL a) Work out the hypotenuse by using Pythagoras. ML = 5 b) Work out angle L by using Trig Sin L = o/h = 4/5 = 0,8 L = 53,13° (key sequence on calculator: 2nd function sin 0,8) c) Work out angle M by using the fact that angles of a triangle add up to 180° M = 180° – 90° – 53,13° = 36,87° |