Hydraulic Jacks

Click here to view a video that explains the hydraulic jack pascal principle.

Hydraulic jacks and many other technological advancements such as automobile brakes and dental chairs work on the basis of Pascal's Principle, named for Blaise Pascal, who lived in the seventeenth century. Basically, the principle states that the pressure in a closed container is the same at all points. Pressure is described mathematically by a Force divided by Area. Therefore, if you have two cylinders connected together, a small one and a large one, and apply a small Force to the small cylinder, this will result in a given pressure. By Pascal's Principle, this pressure would be the same in the larger cylinder, but since the larger cylinder has more area, the force emitted by the second cylinder would be greater. This is represented by rearranging the pressure formula P = F/A, to F = PA. The pressure stayed the same in the second cylinder, but Area was increased, resulting in a larger Force. The greater the differences in the areas of the cylinders, the greater the potential force output of the big cylinder. A hydraulic jack is simply two cylinders connected as described above.

An enclosed fluid under pressure exerts that pressure throughout its volume and against any surface containing it. That's called 'Pascal's Principle', and allows a hydraulic lift to generate large amounts of FORCE from the application of a small FORCE.

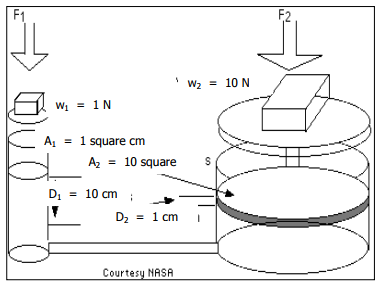
Assume a small piston (one square cm area) applies a weight of 1 N to a confined hydraulic fluid. That provides a pressure of 1 N per square cm throughout the fluid. If another larger piston with an area of 10 square cm is in contact with the fluid, that piston will feel a force of 1 N/ cm² x 10 cm² = 10 N. So, we can apply 1 N to the small piston and get 10 N. of force to lift a heavy object with the large piston. Is this 'getting something for nothing? Unfortunately, no. Just as a lever provides more force near the fulcrum in exchange for more distance further away, the hydraulic lift merely converts work (force x distance) at the smaller piston for the SAME work at the larger one. In the example, when the smaller piston moves a distance of 10 cm it displaces 10 cubic cm of fluid. That 10-cubic cm displaced at the 10-square cm piston moves it only 1 cm, so a small force and larger distance have been exchanged for a large force through a smaller distance.