Page
Cartesian Co-ordinate System
Completion requirements
View
The graphs that you have drawn in previous years are always drawn on a set of axes. These axes have the fancy name of “Cartesian co-ordinate system” and the whole graph is known as a Cartesian plane. The Cartesian co-ordinate system consists of two axes: the horizontal X axis and the vertical Y axis. The X and Y axes cross at 900 at the point zero. This point is also known as the origin.
One can also draw three-dimensional graphs. In this case there are 3 axes: the X, Y and Z axes. The Z axis provides a third dimension in space. We shall, however, only work with X and Y axes. To specify a particular point on a two-dimensional coordinate system, you indicate the x unit first (abscissa), followed by the y unit (ordinate) in the form (x,y), an ordered pair. In three dimensions, a third z unit is added, (x,y,z).
The choices of letters come from the original convention, which is to use the latter part of the alphabet to indicate unknown values. The first part of the alphabet was used to designate known values.
Example:
An example of a point P on the system is indicated in the picture below using the coordinate (5,2).
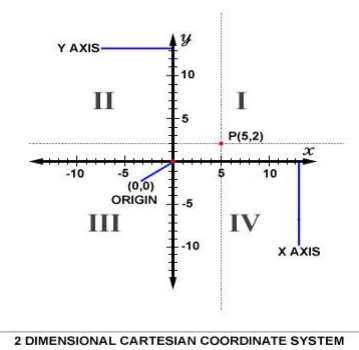
The arrows on the axes indicate that they extend forever in the same direction (i.e. infinitely). The intersection of the two x-y axes creates four quadrants indicated by the roman numerals I, II, III, and IV.
Conventionally, the quadrants are labelled counter clockwise starting from the northeast quadrant. In Quadrant I the values are (x,y), and II:(-x,y), III:(-x,-y) and IV:(x,-y). (see table below)
|
Quadrant |
X values |
Y values |
|
I |
> 0 |
> 0 |
|
II |
< 0 |
> 0 |
|
III |
< 0 |
< 0 |
|
IV |
> 0 |
< 0 |