But first you need to know what an Exponent is.
Here is a quick summary:
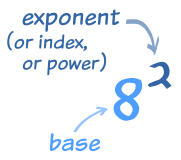
An exponent says how many times to use something in multiplication. In this example: 82 = 8 × 8 = 64
A coefficient is a number used to multiply a variable.
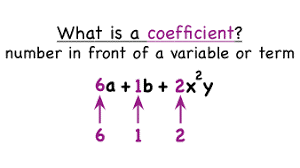
Example: 6z means 6 times z, and “z” is a variable, so 6 is a coefficient.
Exponents
An exponent of 1 means just to have it appear once, so you get the original value:
Example: 81 = 8
An exponent of 0 means not to use it at all, and we have only 1:
Example: 80 = 1
Exponents of (a+b)
Now on to the binomial.
We will use the simple binomial a+b, but it could be any binomial.
Let us start with an exponent of 0 and build upwards.
Exponent of 0
When an exponent is 0, you get1:
(a+b)0=1
Exponent of 1
When the exponent is 1, you get the original value, unchanged:
(a+b)1 = a+b
Exponent of 2
An exponent of 2 means to multiply by itself:
(a+b)2 = (a+b)(a+b) = a2 + 2ab + b2
Exponent of 3
For an exponent of 3 just multiply again:
(a+b)3 = (a+b)(a2 + 2ab + b2) = a3 + 3a2b + 3ab2 + b3
We have enough now to start talking about the pattern.