Our last step is to write it all as a formula.
But hang on, how do we write a formula for "find the coefficient from Pascal's Triangle"?
Well, there is such a formula:
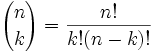
It is commonly called "n choose k" because it is how many ways to choose k elements from a set of n.
You can read more at Combinations and Permutations
The "!" means "factorial", for example 4! = 1×2×3×4 = 24
And it matches Pascal's Triangle like this:
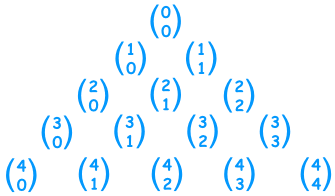
(Note how the top row is row zero and also the leftmost column is zero!)
Example: Row 4, term 2 in Pascal's Triangle is "6".
Let's see if the formula works:
![]()
Yes, it works! Try another value for yourself.
Putting It All Together
The last step is to put all the terms together into one formula.
But we are adding lots of terms together ... can that be done using one formula?
Yes! The handy Sigma Notation allows us to sum up as many terms as we want:
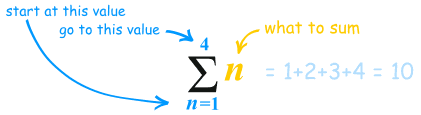
Sigma Notation
Now it can all go into one formula:
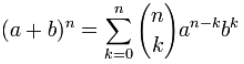
The Binomial Theorem
Use It
OK ... it won't make much sense without an example.
So, let's try using it for n = 3 :
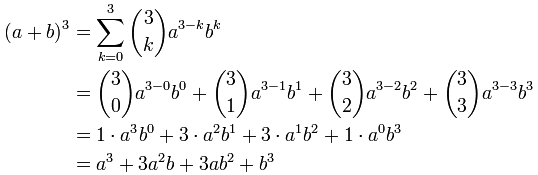
BUT ... it is usually much easier just to remember the patterns:
- The first term's exponents start at n and go down
- The second term's exponents start at 0 and go up
- Coefficients are from Pascal's Triangle, or by calculation using n!/(k!(n-k)!)
Like this:
Example: What is (x+5)4
Start with exponents: x450 x351 x252 x153 x054
Include Coefficients: 1x450 4x351 6x252 4x153 1x054
Then write down the answer (including all calculations, such as 4×5, 6×52, etc):
(x+5)4 = x4 + 20x3 + 150x2 + 500x + 625
You may also want to calculate just one term:
Example: What is the coefficient for x3 in (2x+4)8
The exponents for x3 are: (2x)345
The coefficient is "8 choose 3". We can use Pascal's Triangle, or calculate directly:
n = 8! = 8! = 8×7×6 = 56
k!(n-k)! 3!(8-3)! 3!5! 3×2×1
And we get:
56(2x)345
This simplifies to:
458752 x3
A large coefficient, isn't it?
And one last, most amazing example:
Example: A formula for e (Euler's Number)
You can use the Binomial Theorem to calculate e (Euler's number).
e = 2.718281828459045... (the digits go on forever without repeating)
It can be calculated using:
(1 + 1/n)n
(It gets more accurate the higher the value of n)
That formula is a binomial, right? So let's use the Binomial Theorem:
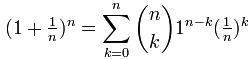
First, we can drop 1n-k as it is always equal to 1:
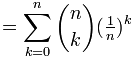
And, quite magically, most of what is left goes to 1 as n goes to infinity:
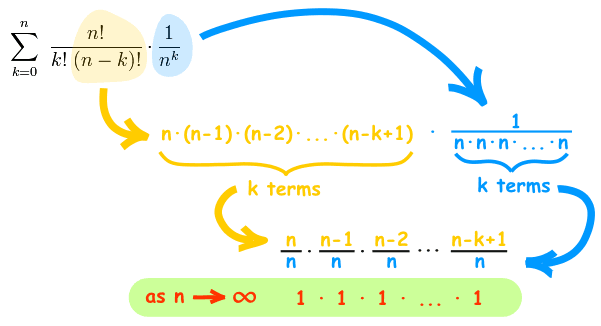
Which just leaves:
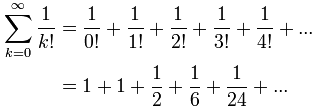
With just those first few terms we get e ≈ 2.7083...
Try calculating more terms for a better approximation!