Definition of a vector: A vector is an object that has both a magnitude and a direction. Geometrically, we can picture a vector as a directed line segment, whose length is the magnitude of the vector and with an arrow indicating the direction. The direction of the vector is from its tail to its head.

The length of the line shows its magnitude and the arrowhead points in the direction.
You can add two vectors by simply joining them head-to-tail:

And it doesn't matter which order you add them, you get the same result:
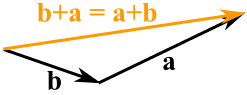
Example: A plane is flying along, pointing North, but there is a wind coming from the North-West.
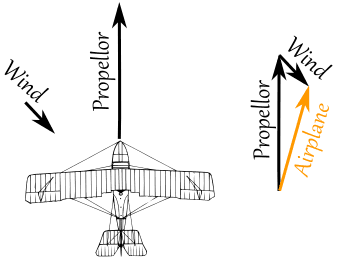
The two vectors (the velocity caused by the propeller, and the velocity of the wind) result in a slightly slower ground speed heading a little East of North.
If you watched the plane from the ground it would seem to be slipping sideways a little.
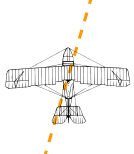
Have you ever seen that happen? Maybe you have seen birds struggling against a strong wind that seems to fly sideways. Vectors help explain that.
Subtracting
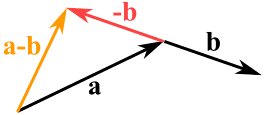
You can also subtract one vector from another:
- First, you reverse the direction of the vector you want to subtract.
- Then add them as usual.
Other Notation
A vector can also be written as the letters of its head and tail with an arrow above, like this:
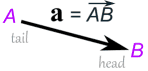
Calculations
Now ... how do we do the calculations?
The most common way is to break up a vector into x and y pieces, like this:
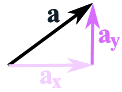
The vector a is broken up into the two vectors ax and ay
Adding Vectors
And here is how to add two vectors after breaking them into x and y parts:
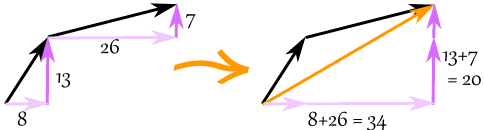
The vector (8,13) and the vector (26,7) add up to the vector (34,20)
Example: add the vectors a = (8,13) and b = (26,7)
c = a + b
c = (8,13) + (26,7) = (8+26,13+7) = (34,20)
Subtracting Vectors
Remember: to subtract, first reverse the vector you want to subtract, then add.
Example: subtract k = (4,5) from v = (12,2)
a = v + -k
a = (12,2) + -(4,5) = (12,2) + (-4,-5) = (12-4,2-5) = (8,-3)
Magnitude of a Vector
The magnitude of a vector is shown by two vertical bars on either side of the vector:
|a|
OR it can be written with double vertical bars (so as not to confuse it with absolute value):
||a||
You can use Pythagoras' theorem to calculate it:
|a| = √( x2 + y2 )
A vector with magnitude 1 is called a Unit Vector.
Vector vs Scalar
When using vectors, we call an ordinary number a "scalar".
Scalar: just a number (like 7 or -0.32) ... definitely not a vector.
A vector is often written in bold, so c is a vector, and it has magnitude and direction but c is just a value, like 3 or 12.4
Example: kb is actually the scalar k times the vector b.
Multiplying a Vector by a Scalar
When you multiply a vector by a scalar it is called "scaling" a vector, because you change how big or small the vector is.
Example: multiply the vector m = (7,3) by the scalar 3.
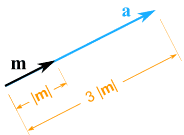
a = 3m = (3×7,3×3) = (21,9)
It still points in the same direction but is 3 times longer.