Page
Special Sequence
Completion requirements
View
Triangular Numbers
1, 3, 6, 10, 15, 21, 28, 36, 45, ...
This Triangular Number Sequence is generated from a pattern of dots that form a triangle.
By adding another row of dots and counting all the dots we can find the next number of the sequence:
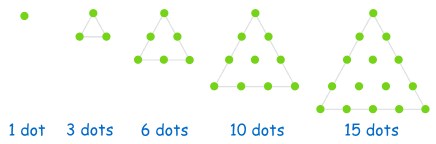
Square Numbers
0, 1, 4, 9, 16, 25, 36, 49, 64, 81, ...
They are the squares of numbers:
0 (=0×0)
1 (=1×1)
4 (=2×2)
9 (=3×3)
16 (=4×4) etc...
Cube Numbers
0, 1, 8, 27, 64, 125, 216, 343, 512, 729, ...
They are the cubes of numbers:
0 (=0×0×0)
1 (=1×1×1)
8 (=2×2×2)
27 (=3×3×3)
64 (=4×4×4) etc...
Fibonacci Numbers
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
The Fibonacci Sequence is found by adding the two numbers before it together.
The 2 is found by adding the two numbers before it (1+1)
The 21 is found by adding the two numbers before it (8+13)
The next number in the sequence above would be 55 (21+34)
Can you figure out the next few numbers?
Other Sequences
There are lots more! You might even think of your own ...
Inverse Functions
An inverse function goes in the opposite direction!
Let us start with an example:
Here we have the function f(x) = 2x+3, written as a flow diagram:
The Inverse Function just goes the other way:
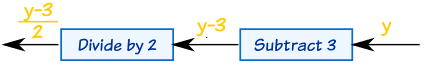
So the inverse of 2x+3 is: (y-3)/2
The inverse is usually shown by putting a little "-1" after the function name, like this:
f-1(y)
We say "f inverse of y"
So, the inverse of f(x) = 2x+3 is written:
f-1(y) = (y-3)/2
(I also used y instead of x to show that we are using a different value.)
Back to Where We Started
The cool thing about the inverse is that it should give you back the original value:
If the function f turns the apple into a banana, Then the inverse function f-1 turns the banana back to the apple
Example:
Using the formulas from above, we can start with x=4:
f(4) = 2×4+3 = 11
We can then use the inverse on the 11:
f-1(11) = (11-3)/2 = 4
And we magically get 4 back again!
We can write that in one line:
f-1( f(4) ) = 4
"f inverse of f of 4 equals 4"
So, applying a function f and then its inverse f-1 gives us the original value back again:
f-1( f(x) ) = x
We could also have put the functions in the other order and it still works:
f( f-1(x) ) = x
Example:
Start with:
f-1(11) = (11-3)/2 = 4
And then:
f(4) = 2×4+3 = 11
So, we can say:
f( f-1(11) ) = 11 "f of f inverse of 11 equals 11"
Solve Using Algebra
You can work out the inverse using Algebra. Put "y" for "f(x)" and solve for x:
The function: f(x) = 2x+3
Put "y" for "f(x)": y = 2x+3
Subtract 3 from both sides: y-3 = 2x
Divide both sides by 2: (y-3)/2 = x
Swap sides: x = (y-3)/2
Solution (put "f-1(y)" for "x") : f-1(y) = (y-3)/2
This method works well for more difficult inverses.