Inverses of Common Functions

It has been easy so far because we know the inverse of Multiply is Divide, and the inverse of Add is Subtract, but what about other functions?

Here is a list to help you:

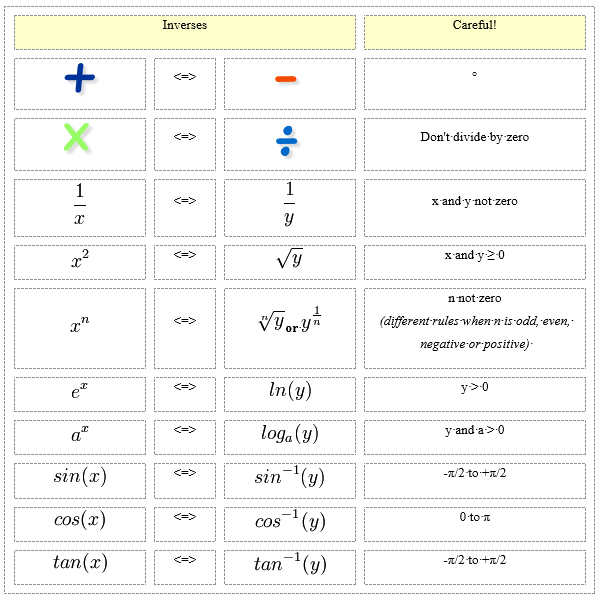
(Note: you can read more about Inverse Sine, Cosine and Tangent.)

Did you see the "Careful!" column above? That is because some inverses work only with certain values.

Example: Square and Square Root

If you square a negative number and then do the inverse this happens:

Square: (-2)² = 4

Inverse (Square Root): √(4) = 2

But we didn't get the original value back! We got 2 instead of -2. Our fault for not being careful!

So, the square function (as it stands) does not have an inverse

But we can fix that!

Restrict the Domain (the values that can go into a function).

Example: (continued)

Just make sure you don't use negative numbers.

In other words, restrict it to x ≥ 0 and then you can have an inverse.

So we have this situation:

x² does not have an inverse

but {x² | x ≥ 0 } (which says "x squared such that x is greater than or equal to zero" using set-builder notation) does have an inverse.

Why Would There Be No Inverse?

Let us see graphically what is going on here:

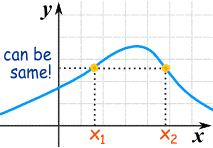
To be able to have an inverse you need unique values.

Just think ... if there are two or more x-values for one y-value, how do you know which one to choose when going back?

No Inverse

Inverse is Possible

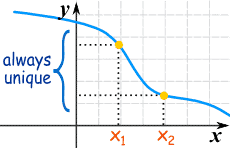When a y-value has more than one x-value, how do you know which x-value to go back to?	When there is a unique y-value for every x-value you can always "go back" from y to x.

So, we have this idea of "a unique y-value for every x-value", and it actually has a name. It is called "Injective" or "One-to-one":

If a function is "One-to-one" (Injective) it has an inverse.

Click here to view a video that explains inverse functions.