Domain and Range

So what is all this talk about "Restricting the Domain"?

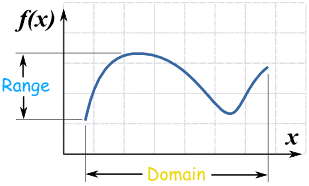
In its simplest form, the domain is all the values that go into a function (and the range is all the values that come out).

As it stands the function above does not have an inverse.

But you could restrict the domain so there is a unique y for every x ...

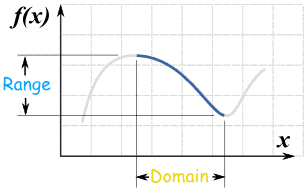
... and now you can have an inverse:

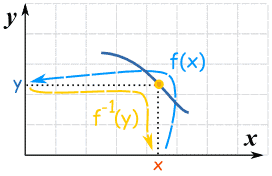
Note also:

 The function f(x) goes from the domain to the range,

The inverse function f^-1(y) goes from the range back to the domain.

Or...

You could plot them both in terms of x ... so it is now f^-1(x), not f^-1(y)

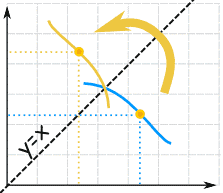
f(x) and f^-1(x) are like mirror images (flipped about the diagonal).

In other words:

The graph of f(x) and f^-1(x) are symmetric across the line y=x

Example: Square and Square Root (continued)

First, we restrict the Domain to x ≥ 0:

{x² | x ≥ 0 } "x squared such that x is greater than or equal to zero"

{√x | x ≥ 0 } "square root of x such that x is greater than or equal to zero"

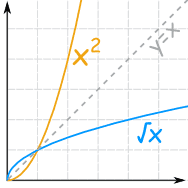
And you can see they are "mirror images" of each other about the diagonal y=x.

Note: we could have restricted the domain to x ≤ 0 and the inverse would then be f^-1(x) = -√x:

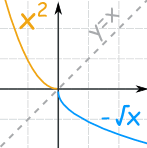
{x² | x ≤ 0 }

{-√x | x ≥ 0 }

Which are inverses, too.

Not Always Solvable!

It is sometimes not possible to find an Inverse of a Function.

Example: f(x) = x/2 + sin(x)

We cannot work out the inverse of this, because we cannot solve for "x":

y = x/2 + sin(x)

y ... ? = x

Notes on Notation

Even though we write f^-1(x), the "-1" is not an exponent (or power):

f^-1(x) ...is different to... f(x)^-1

Inverse of the function f f(x)^-1 = 1/f(x) (the Reciprocal)

Summary

The inverse of f(x) is f^-1(y)

You can find an inverse by reversing the "flow diagram"

Or you can find an inverse by using Algebra:

Put "y" for "f(x)", and

Solve for x

You may need to restrict the domain for the function to have an inverse.

Click here to view a video that explains restricting the domain of a function to make it invertible.