A Sequence is a set of things (usually numbers) that are in order.
Infinite Or Finite
If the sequence goes on forever it is called an infinite sequence, otherwise, it is a finite sequence
Examples:
{1, 2, 3, 4 ,...} is a very simple sequence (and it is an infinite sequence)
{20, 25, 30, 35, ...} is also an infinite sequence
{1, 3, 5, 7} is the sequence of the first 4 odd numbers (and is a finite sequence)
{4, 3, 2, 1} is 4 to 1 backwards
{1, 2, 4, 8, 16, 32, ...} is an infinite sequence where every term double
{a, b, c, d, e} is the sequence of the first 5 letters alphabetically
{f, r, e, d} is the sequence of letters in the name "fred"
{0, 1, 0, 1, 0, 1, ...} is the sequence of alternating 0s and 1s (yes, they are in order, it is an alternating order in this case)
The Characteristics Of A Number Sequence:
In Order: When we say the terms are "in order", we are free to define what order that is! They could go forwards, backwards ... or they could alternate ... or any type of order you want!
Like a Set: A Sequence is like a Set, except the terms are in order (with Sets the order does not matter) the same value can appear many times (only once in Sets)
Example: {0, 1, 0, 1, 0, 1, ...} is the sequence of alternating 0s and 1s.
The set would be just {0,1}
Notation
Sequences also use the same notation assets: list each element, separated by a comma, and then put curly brackets around the whole thing.
{3, 5, 7, ...} The curly brackets { } are sometimes called "set brackets" or "braces".
A Rule
A Sequence usually has a Rule, which is a way to find the value of each term.
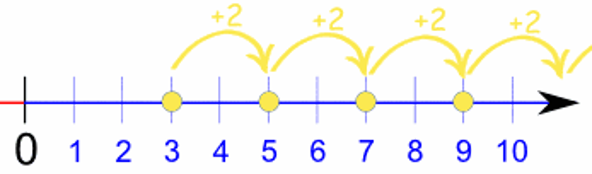
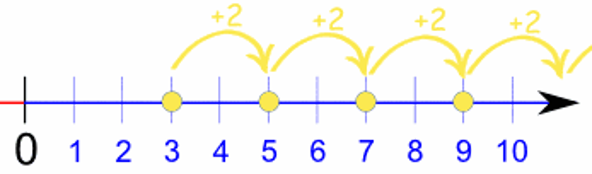
Example: the sequence {3, 5, 7, 9, ...} starts at 3 and jumps 2 every time:
Can be Expressed as a Formula
Saying "starts at 3 and jumps 2 every time" is fine, but it doesn't help us calculate the:
- 10th term,
- 100th term, or
- nth term, where n could be any term number we want.
So, we want a formula with "n" in it (where n is any term number).
So, What Would A Rule For {3, 5, 7, 9, ...} Be?
Firstly, we can see the sequence goes up 2 every time, so we can guess that a Rule will be something like "2 times n" (where "n" is the term number). Let's test it out:
Test Rule: 2n
|
n |
Term |
Test Rule |
|
1 |
3 |
2n = 2×1 = 2 |
|
2 |
5 |
2n = 2×2 = 4 |
|
3 |
7 |
2n = 2×3 = 6 |
That nearly worked ... but it is too low by 1 every time, so let us try changing it to:
Test Rule: 2n+1
|
n |
Term |
Test Rule |
|
1 |
3 |
2n+1 = 2×1 + 1 = 3 |
|
2 |
5 |
2n+1 = 2×2 + 1 = 5 |
|
3 |
7 |
2n+1 = 2×3 + 1 = 7 |
That Works!
So instead of saying "starts at 3 and jumps 2 every time" we write this: 2n+1
Now we can calculate, for example, the 100th term: 2 × 100 + 1 = 201
Many Rules
But mathematics is so powerful we can find more than one Rule that works for any sequence.
Example: the sequence {3, 5, 7, 9, ...}
We have just shown a Rule for {3, 5, 7, 9, ...} is: 2n+1
And so we get: {3, 5, 7, 9, 11, 13, ...}
But can we find another rule?
How about "odd numbers without a 1 in them":
And we would get: {3, 5, 7, 9, 23, 25, ...}
A Completely Different Sequence!
And we could find more rules that match {3, 5, 7, 9, ...}. Really, we could.
So it is best to say "A Rule" rather than "The Rule" (unless you know it is the right Rule).
Notation
To make it easier to use rules, we often use this special style:
 |
xn is the term n is the term number |
For example: to mention the "5th term" you just write: x5
So a rule for {3, 5, 7, 9, ...} can be written as an equation like this:
xn = 2n+1
And to calculate the 10th term we can write:
x10 = 2n+1 = 2×10+1 = 21
Can you calculate x50 (the 50th term) doing this?
Here is another example:
Calculate the First 4 Terms Of This Sequence
{an} = {(-1/n)n }
Calculations:
a1 = (-1/1)1 = -1
a2 = (-1/2)2 = 1/4
a3 = (-1/3)3 = -1/27
a4 = (-1/4)4 = 1/256
Answer:
{an} = { -1, 1/4, -1/27, 1/256, ... }
Special Sequences
Now let's look at some special sequences and their rules.
Arithmetic Sequences
In an Arithmetic Sequence, the difference between one term and the next is a constant.
In other words, you just add some value each time ... on to infinity.
Example:
1, 4, 7, 10, 13, 16, 19, 22, 25, ...
This sequence has a difference of 3 between each number.
Its Rule is xn = 3n-2
In General, you could write an arithmetic sequence like this:
{a, a+d, a+2d, a+3d, ... }
where:
a is the first term, and
d is the difference between the terms (called the "common difference")
And you can make the rule by:
xn = a + d(n-1)
(We use "n-1" because d is not used in the 1st term).
Geometric Sequences
In a Geometric Sequence, each term is found by multiplying the previous term by a constant.
Example:
2, 4, 8, 16, 32, 64, 128, 256, ...
This sequence has a factor of 2 between each number.
Its Rule is xn = 2n
In General, you could write a geometric sequence like this:
{a, ar, ar2, ar3, ... }
where:
- a is the first term, and
- r is the factor between the terms (called the "common ratio")
Note: r should not be 0.
When r=0, you get the sequence {a,0,0,...} which is not geometric
And the rule is:
xn = ar(n-1)
(We use "n-1" because ar0 is the 1st term)