Completion requirements
View
In the last result we got:
a3 + 3a2b + 3ab2 + b3
Now, notice the exponents of a. They start at 3 and go down: 3, 2, 1, 0:
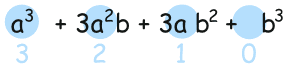
Likewise, the exponents of b go upwards: 0, 1, 2, 3:
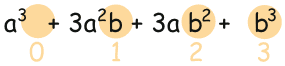
If we number the terms 0 to n, we get this:
|
k=0 |
k=1 |
k=2 |
k=3 |
|
a3 |
a2 |
a |
1 |
|
1 |
b |
b2 |
b3 |
Which can be brought together into this:
an-kbk
How about an example to see how it works?
Example: When the exponent, n, is 3.
The terms are:
|
k=0: |
k=1: |
k=2: |
k=3: |
|
an-kbk |
an-kbk |
an-kbk |
an-kbk |
It works like magic!