Coefficient

So far we have: a³ + a²b + ab² + b³

But we really need: a³ + 3a²b + 3ab² + b³

We are missing the numbers (which are called coefficients).

Let's look at all the results we got before, from (a+b)⁰ up to (a+b)³:

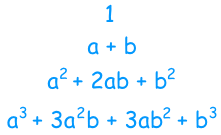
And now look at just the coefficients (with a "1" where a coefficient wasn't shown):

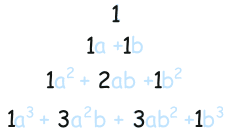
They actually make Pascal's Triangle!

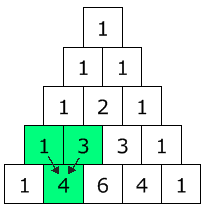
Each number is just the two numbers above it added together (except for the edges, which are all "1")

(Here I have highlighted that 1+3 = 4)

Armed with this information let us try something new ... an exponent of 4:

a exponent go 4,3,2,1,0: a⁴ + a³ + a² + a + 1

b exponents go 0,1,2,3,4: a⁴ + a³b + a²b² + ab³ + b⁴

Coefficients go 1,4,6,4,1: a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

And that is the correct answer.

We have success!

We can now use that pattern for exponents of 5, 6, 7, ... 50, ... 112, ... you name it!