Pythagoras Theorem

Years ago, a man named Pythagoras found an amazing fact about triangles:

If the triangle had a right angle (90°) ...

... and you made a square on each of the three sides, then ...

... the biggest square had the exact same area as the other two squares put together!

Pythagoras’ theorem is mainly used to calculate height and distance for example.

Definition

The longest side of the triangle is called the "hypotenuse", so the formal definition is:

In a right-angled triangle: the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Let's see if it really works using an example.

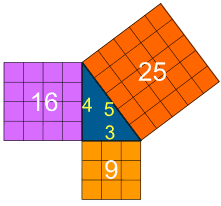
Let's check if the areas are the same:

3² + 4² = 5²

Calculating this becomes:

9 + 16 = 25

It works ... like Magic!

Why Is This Useful?

If we know the lengths of two sides of a right-angled triangle, we can find the length of the third side. (But remember it only works on right-angled triangles!)

How Do I Use It?

Write it down as an equation:

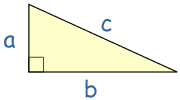
a² + b² = c²

Now you can use algebra to find any missing value, as in the following examples:

a² + b² = c²

5² + 12² = c²

25 + 144 = c²

169 = c²

c2 = 169

c = √169

c = 13

You can also read about Squares and Square Roots to find out why √169 = 13

a² + b² = c²

9² + b² = 15²

81 + b² = 225

Take 81 from both sides:

b² = 144

b = √144

b = 12

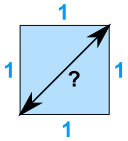
a² + b² = c²

1² + 12 = c²

1 + 1 = c²

2 = c²

c² = 2

c = √2 = 1.4142...

It works the other way around, too: when the three sides of a triangle make a2 + b2 = c2, then the triangle is right-angled.

Does this triangle have a Right Angle?

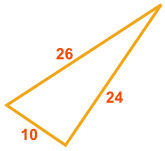
Does a² + b² = c² ?

a² + b² = 10² + 24² = 100 + 576 = 676

c² = 26² = 676

They are equal, so ...

Yes, it does have a Right Angle!

Do an 8, 15, 16 triangles have a Right Angle?

Does 8² + 15² = 16² ?

8² + 15² = 64 + 225 = 289,

but 16² = 256

So, NO, it does not have a Right Angle

Example: Does this triangle have a Right Angle?

In the below example, let the length of the sides be 4 cm. Draw the altitude from B forming BD. The altitudes drawn in an equilateral and isosceles triangle touch the midpoint of the opposite side dividing the side into two equal halves and form two right-angled triangles.

Equivalent Triangle

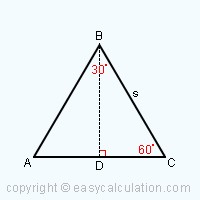
Let us take BDC to find the height (BD) with DC being 2 cm (half of AC).

BC² = BD² + DC²

4² = BD² + 2²

BD² = 16 - 4

BD² = 12

BD = 3.46

Hence the height of the above equilateral is 3.46 cm.

Click here to view a video that explains the Pythagorean Theorem.