Pythagoras Theorem

Years ago a man named Pythagoras found an amazing fact about triangles:

If the triangle had a right angle (90°),

and you made a square on each of the three sides, then...

the biggest square had the exact same area as the other two squares put together!

Pythagoras’ theorem is mainly used to calculate height and distance.

Definition

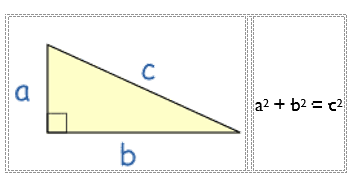
The longest side of the triangle is called the "hypotenuse", so the formal definition is:

In a right-angled triangle,

• the square of the hypotenuse is equal to
• the sum of the squares of the other two sides.

Let's see if it really works by using an example.

Why Is This Useful? If we know the lengths of the two sides of a right-angled triangle, we can find the length of the third side. (But remember it only works on right-angled triangles!)

How Do I Use It? Write it down as an equation:

Now you can use algebra to find any missing value, as in the following examples:

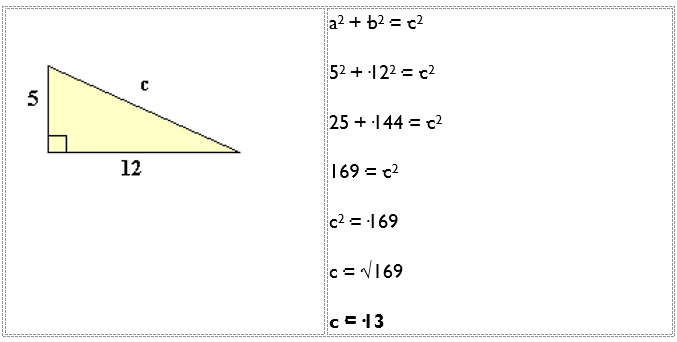
You can also read about Squares and Square Roots to find out why √169 = 13

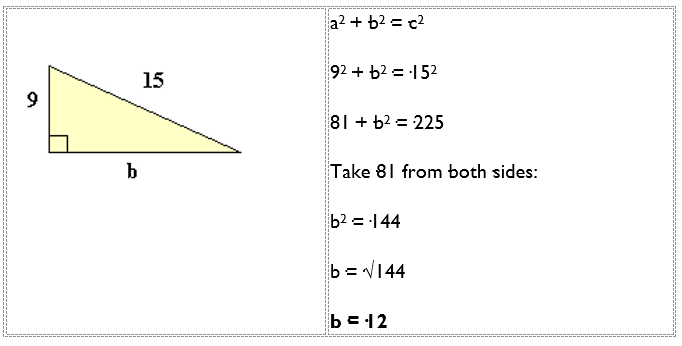
It works the other way around too: when the three sides of a triangle make a2 + b2 = c2, then the triangle is right-angled.

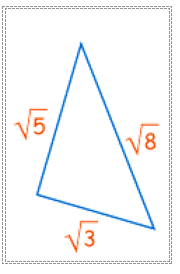
Does this triangle have a right angle?

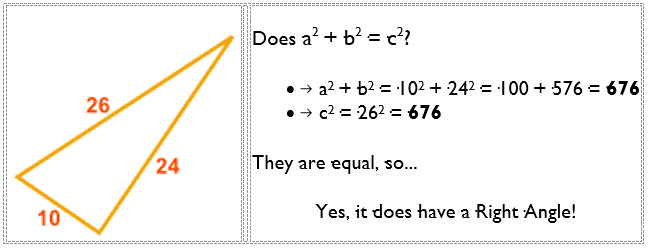
Do triangles 8, 15, 16 have a right angle?

Does 8² + 15² = 16² ?

8² + 15² = 64 + 225 = 289,

but 16² = 256

So, NO, it does not have a right angle.

Example: Does this triangle have a right angle?

In the below example, let the length of the sides be 4 cm. Draw the altitude from B forming BD. The altitudes are drawn in an equilateral and isosceles triangle touch the midpoint of the opposite side dividing the side into two equal halves and form two right-angled triangles.

Equivalent Triangle

Let us take BDC to find the height (BD) with DC being 2 cm (half of AC).

BC² = BD2 + DC²

4² = BD² + 2²

BD² = 16 - 4

BD² = 1²

BD = 3.46

Hence the height of the above equilateral is 3.46 cm.